Hledání místa s nejnižší hustotou

[abuki]

Ahoj,

potřeboval bych navést, pravděpodobně bude existovat nějaký algoritmus?
Mám plochu (jsem ve 2d) a na ní umístěné obdélníky (ale pro jednoduchost klidně můžeme říct body - středy obdélníků) a já hledám místo na té ploše, kde je nejmenší hustota těch bodů/obdélníků.

Nebo-li mám stůl s rozházenejma kartama a když přidávám další kartu tak chci najít nějaký nejvíc prázdný místo, kam plácnout novou kartu.

Stačila by mi asi nějaká fakt jednoduchá aproximace, nepotřebuju nic přesného, spíš jednoduchého a rychlého.
_________________
Twitter @abukac
www.amanita-design.net
www.circusatos.com

[pcmaster]

Strelim od brucha.

Vytvor si uniform-grid s nejakym vhodnym rozlisenim. V kazdej bunke budes mat pocet stredov obdlznikov, ktore tam padli (vyroba: O(n)). Bunku s minimalnou hodnotou uz zistis velmi jednoducho. A mozes si v pripade, ze ich je viac, vybrat tu najblizsie k stredu. A tam uz urobit presnu koliziu s kartami, aby si zistil, ci ti to tam fakt vlezie. Bude to sakra rychle

Pripadne nad tym (ci namiesto toho) mozes postavit nejaku hierarchicku strukturu (multi-level uniform-grid pripadne strom (kD, BVH, BSP, quad, ...)). Ale nekomplikoval by som to
_________________
Off-topic flame-war addict since the very beginning. Registered since Oct. 2003!
Interproductum fimi omne est.

[]semo[]

Nebo použít "multiple choice algoritmus": náhodně vygeneruješ X míst, ohodnotíš je a vybereš to nejlepší z nich. Ohodnocení by mohlo spočívat v nějaké funkci vzdáleností obdélníků a bodu (minimální vzdálenost, medián...?).

Jinou možnost bych viděl v nějakým odpuzování bodu. Hodit bod do plochy a provést N iterací, přičemž v každé iteraci by každý obdélník odpuzoval tento bod od svého středu (silou přímo úměrnou velikost plochy toho obdélníku). Po několika iteracích bude bod na správném místě.
_________________
Kdo jede na tygru, nesmí sesednout.
---
http://www.inventurakrajiny.cz/sipka/
Aquadelic GT, Mafia II, simulátory

[micky]

A nebo použít Voronoi diagram/Delaunay triangulaci, přes něj se dá najít největší prázdná kružnice.



Ale ten uniform grid bude na implementaci jednodušší...
_________________
https://www.bluepulsar.cz/
https://twitter.com/11thDream_Game/

[Radis]

Urcite se priklanim k pcmasterovi, vsechno ostatni je overkill. Pridani karty je O(1) a je to jednoduche na implementaci. Kdysi jsem neco podobneho resil presne timto zpusobem (dva gridy "pres sebe" - vetsi a mensi bunky).

[]semo[]

Naopak mřížka je overkill. Buď ji musíš vždy vytvořit znovu, nebo řešit nějaký updaty pozic obdélníků (přesun, odebrání). Navíc bys musel laborovat s velikostí. I ta složitost O(1) neni podle mě pravda (nejde o přidání, ale o dotaz na volné místo). Ale je to intuitivní a fungovat to bude, o tom žádná.

Delaunay sice overkill taky je, ale je to skvělý nápad. Najde to skutečně dobré místo. Záleží, na co bys to potřeboval a jak přesně.

Multiple choice by mohl být na implementaci nejjednodušší a přitom by byl i dostatečně škálovatelný a rychlý.

Odpuzování bodu bude ve výsledku rychlé taky, i když má více průchodů. Iterace provádíš nad menší pamětí, která by mohla být navíc při dalším průchodu dobře nakešovaná (pokud zrovna nebudeš procházet pole pointerů na obdélníky, ale uložíš se pozice do pole).


Já bych to trochu zkombinoval: rozházel pár bodů náhodně, pár bodů podle mřížky, párkrát bych je odpudil těma kartma a nakonec bych vybral ten nejlepší :-D. A ten bych vložil do Delaunayovi triangulace, aby micky nebyl smutný ;-).
_________________
Kdo jede na tygru, nesmí sesednout.
---
http://www.inventurakrajiny.cz/sipka/
Aquadelic GT, Mafia II, simulátory

[abuki]

Díky všam za návhry.

Multiple choice mi přijde nejjednodušší. Nicméně se vlastně trochu bojim tý šance na nepřesnost.

U mřížky si řikám, že bude snadný trefit buňku, která je sice prázdná, ale hraničí s hromadou jiných. Nevím jestli bych pak nemusel počítat celý obsah obdélníku (ne jen jeho střed) a tím by se to asi dost zkomplikovalo.

Voronoi už jsem viděl v nějakym příkladu pro generování levelů, tak možná nakonec půjdu do toho. Sice to je možná overkill, ale zas bych do toho rád proniknul.

micky: můžeš mě navést jak se to počítá? Normálně docela obstojně googlim, ale v matematickýh koutech internetu mi to moc nejde.
_________________
Twitter @abukac
www.amanita-design.net
www.circusatos.com

[abuki]

Je totiž fakt, že by bylo pěkný, kdyby se ta karta fakt dala na nejprázdnější místo, což odpovídá středu té nejprázdnější kružnice.
_________________
Twitter @abukac
www.amanita-design.net
www.circusatos.com

[Radis]

[mar]

[]semo[]

[micky]

Ono je to hezky vidět na Voronoi, ale implementoval bych to asi přes Delaunayho triangulaci, jak říkal ]semo[. Je to de facto ta samá struktura, jen jsou spojeny středy buněk úsečkami a tvoří tak trojúhelníkovou síť.



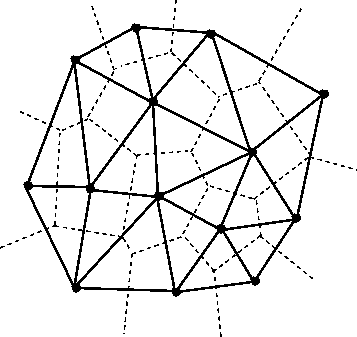
Vlastností Delaunay je, že kružnice opsaná kolem libovolného trojúhelníku neobsahuje žádný vrchol jiného trojúhelníku.



Algoritmy/ukázky sestrojení jsou na internetu, určitě budou lepší než moje polovičaté vysvětlení v pár větách. Nic složitého to opravdu není.

Pak stačí všechny ty trojúhelníky projít a vybrat ten s největší kružnicí opsanou. Na to jsou vzorečky.

https://www.mathopenref.com/trianglecircumcircle.html

Do toho trojúhelníku vložíš nový bod/kartu. Může to být přesně do středu té kružnice opsané, ale trochu randomizovat není ve hře na škodu. Vkládání do Delaunay sítě se dá opět někde vyhledat. Druhá možnost je jí zkonstruovat celou znovu, nečekám, že budeš mít na ploše desetitisíce karet.

Osobně se mi teď líbí nejvíc ta semova iterativní metoda, jen by se muselo dát bacha, aby ta karta neodputovala pryč z obrazu. Vyladit parametry.
_________________
https://www.bluepulsar.cz/
https://twitter.com/11thDream_Game/

[micky]

Proboha, matematická otázka a my se můžem přetrhnout

V rastru jsem si s tím kdysi hrál, na školním webu je to pořád dostupné. http://home.zcu.cz/~zakm7/voronoi/
_________________
https://www.bluepulsar.cz/
https://twitter.com/11thDream_Game/

[abuki]

Bohužel jsem zjistil, že vlastně asi nakonec to místo s nejmenší hustotou nehledám
Asi budu dávat kartu vždy na stejné místo (kvůli konsistenci UX), ale vyřeším to tím, že kam dopadne, tam se ty ostatní odsunou trochu stranou.

Ale je mi to skoro až líto, protože jste tady popsali dost zajímavý věci. Ale asi si na to budu muset vymyslet jinou hru
_________________
Twitter @abukac
www.amanita-design.net
www.circusatos.com

[micky]

Použij, co bude pro hru/aplikaci nejlepší. My už jsme si zamachrovali a jsme spokojení.
_________________
https://www.bluepulsar.cz/
https://twitter.com/11thDream_Game/